Inspired by this question.

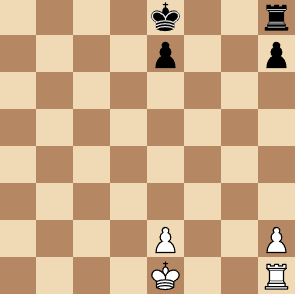
This question will proceed on the assumption that the position depicted is a draw, and that it's possible to prove this by enumerating a set of white-to-move positions that:

1. Includes the above

2. Includes all one-ply follow-ons with colors flipped

3. Is such that for any position in the set, there is a move for white such that any response to the move by black leads back to a position in the set.

This question asks, what is the minimal size of a set with this property?

Note that "position" includes castling and en passant data, but not half-move counter data.

Individual answers resolve when proof is provided in the comments that they should resolve a particular way.