
This is a derivative question; it will resolve exactly according to these questions:
/ManifoldPolitics/will-trump-win-the-2024-election
/EvanDaniel/will-elon-musk-spend-a-night-in-pri
It will resolve yes if those questions resolve in different ways. That is, if Trump wins and Elon stays out of jail, or Trump loses and Elon goes to jail, this will resolve Yes. If the questions resolve in the same way, this question will resolve No.
I feel like anyone who sees this market linked somewhere other than Manifold is going to think it's a straight-up conditional market, and that this means Elon has a really high chance of going to jail if Trump loses. I know there's not much space for the title due to the small character limit, but might be good to make it more clear that's not what this is. Something like, "Will Trump lose and Elon go to jail, or Trump wins and he stays out of jail?"
TBH I'm starting to think it would be better to just have a regular conditional market. “If Trump loses, will Elon spend a night in jail by EOY 2026?” (resolves N/A if Trump wins) tests Elon Musk’s claim directly, and gives you the conditional probability of Elon spending a night in jail given that Trump loses. You can then calculate the “iff” probability based on that one and the other two markets listed in the description (see my other comment). I think making it so that each trader has to do the math themselves may lead to some inefficiency.
I think the current, more intuitive title helps, but note how the current value (46%) still implies that people think a Trump victory makes Elon more likely to go to jail. (For reference, if they thought the result of election didn't affect Elon’s fate at all, it should be at 47.5%, and higher if they agreed with Elon with regards to the direction of the effect).
@santiago You can't arb N/A markets, for starters. They suck in far more ways than that, though, as others have written about at great length.
I'm sympathetic to the idea that titles should help people understand the thing, but at some point I think it's reasonable for participants in a market to have to actually understand what they're trading on and maybe do a touch of math. If they're getting it wrong, stop complaining and go take their money!
There are plenty of markets on the site using the N/A approach. It's fine to have a few that intentionally avoid it. Ideally we'd have software / UI support for derivative markets and such, and you could place the conditional bet on a market that won't resolve N/A as easily as you currently can on one that might. But we're not there yet, so I'll do the best I can...
The title technically doesn't match the description. The title implies a relationship that is impossible to prove. The description describes a simple XNOR table that is easy to resolve. A more accurate title would be: "Will Elon spend a night in jail by EOY 2026 if Trump loses, or not if not?" That's to keep it short, which I assume is why you chose to use the abbreviation "iff". If you want to make it sound more natural, options include:
"Will Elon spend a night in jail by EOY 2026 if Trump loses, or not if Trump wins?" (my preference)
"Will Elon spend a night in jail by EOY 2026 if Trump loses, or avoid jail if not?" (technically requires additional clarification because "avoid jail" isn't necessarily the negation of "spend a night in jail", i.e. you could spend less than a night in jail, but not avoid it. But the implication is obvious.)
"Will Elon spend a night in jail by EOY 2026 if Trump loses, or avoid jail if Trump wins?" (most verbose, same "issue" as previous one)
You can really write it however you want, like "Will Elon spend a night in jail by EOY 2026 if Trump loses, or will he not if Trump wins?" (my preference but more verbose)
You can remove the verbosity and switch up the negations too: "Will Elon spend a night in jail by EOY 2026 if Trump loses, or not otherwise?"
"Will Elon spend a night in jail by EOY 2026 if Trump loses, or not if wins?"
Endless combinations without the technically incorrect jargon.
As per usual, the description trumps the title, but I see this as an unintended clickbait market where people see the percentage high but don't notice the second F in the title (or don't know what it means and assume it's a typo).
Here's the rationale: https://chatgpt.com/share/67072fd1-6c24-8001-bd74-ff5208e779bd
@PeterNjeim Thanks, I like several of those title suggestions! I'll ponder them and make some edits.
That said, I strongly disagree with this part:
The title technically doesn't match the description. The title implies a relationship that is impossible to prove.
This isn't true. There are multiple ways to provide the proof. Quoting the Wiki article linked below, which matches my recollections from math classes:
An alternative is to prove the disjunction "(P and Q) or (not-P and not-Q)", which itself can be inferred directly from either of its disjuncts—that is, because "iff" is truth-functional, "P iff Q" follows if P and Q have been shown to be both true, or both false.
We can't prove the relationship yet, but once the underlyings have resolved we will be able to prove or disprove the disjunction by examination. That's why the truth table given in that article matches the one in my description.
A possibly more intuitive way to think about it is: what set of outcomes in the real world would disprove the double implication in the title (and thus resolve this question No)?
@PeterNjeim As always, chatpgt can make mistakes. I'm willing to believe "chatgpt getting confused implies lots of normal people will get confused", but that does not make either chatgpt or those people correct.
When led to the right answer, chatgpt can recognize its mistakes:
https://chatgpt.com/share/67075370-c484-800b-b0d4-696570f7e2c0
@EvanDaniel Thanks for reading my comments. However, for the logic question, the problem is deeper than that, see this for some food for thought: https://chatgpt.com/share/6707587d-d810-8001-a1e5-978774b28f8a
@PeterNjeim It's not especially deeper than that. Once you know the answers to the underlyings, iff is just a truth table. Yes, you can talk ChatGPT into silliness if you want. No, I'm not interested in arguing with it vicariously. IFF is a logical connective; any reading of causation or whatever other asymmetric weirdness is a you problem.
@PeterNjeim 'A iff B' is a truth-functional connective. It doesn't care about whether the propositions are "eternally linked" any more than negation ('not A') cares about whether A is 'eternally false' or conjunction ('A and B') cares about A and B being being 'eternally both true'.
If you want to capture the notion that that under all possible worlds A and B have the same truth-value, you would use subjunctive conditionals instead of indicative conditionals. But I don't think I have ever seen 'iff' used for subjunctive conditionals.
@Wotton thank you for your explanation
It was a different interpretation of the title that led to the differing views, more details here: https://chatgpt.com/share/67076f58-4518-8001-9508-84e29c91876d
@EvanDaniel Ehhh, the "Will X if Y, or not if Z" format could easily be interpreted as if those are the two distinct outcomes the market is evaluating. (That is, resolves one way if X & Y, another if ~X & Z, and maybe implicitly N/A if neither.) I don't think there's really a clean way around relying on the "if and only if" concept; maybe just use "⇔" or ("⟺" or "≡")? A lot of people wouldn't understand the meaning, but they wouldn't misunderstand it as meaning something else, at least.
@UnspecifiedPerson It is clean though. "Trump wins" is the negation of "Trump loses". It's "(X and Y) or (!X and !Y)", which is the same as XNOR, as shown in Evan's citation of the Wikipedia article earlier. If "Trump wins" truly was Z and not !Y, you'd be right, but in this case all cases are covered
@lxgr I guess a positive EV position and being neutrally hedged are two different things then? ¯\_(ツ)_/¯
TL;DR Given the current values of other markets, this one should be at between 32% and 62%. It's way too low now.
So, since this is equivalent to
(Trump wins AND Elon stays out of jail) OR (Trump loses AND Elon goes to jail)
the probability of this resolving to YES is given by
P(YES) = P(Elon out of jail | Trump wins) × P(Trump wins) + P(Elon in jail | Trump loses) × P(Trump loses)
(where P(A|B) is the probability of A happening given that B happens). We know that
P(Elon in jail) = P(Elon in jail | Trump wins) × P(Trump wins) + P(Elon in jail | Trump loses) × P(Trump loses)
If we take the values P(Elon in jail) = 15% and P(Trump wins) = 47%, which is where they are at currently in the other markets, we get that
15% = P(Elon in jail | Trump wins) × 47% + P(Elon in jail | Trump loses) × 53%
This means that P(Elon in jail | Trump wins) must be between 0% and 32% (and thus P(Elon out of jail | Trump wins) is between 68% and 100%), and P(Elon in jail | Trump loses) must be between 0% and 28%:
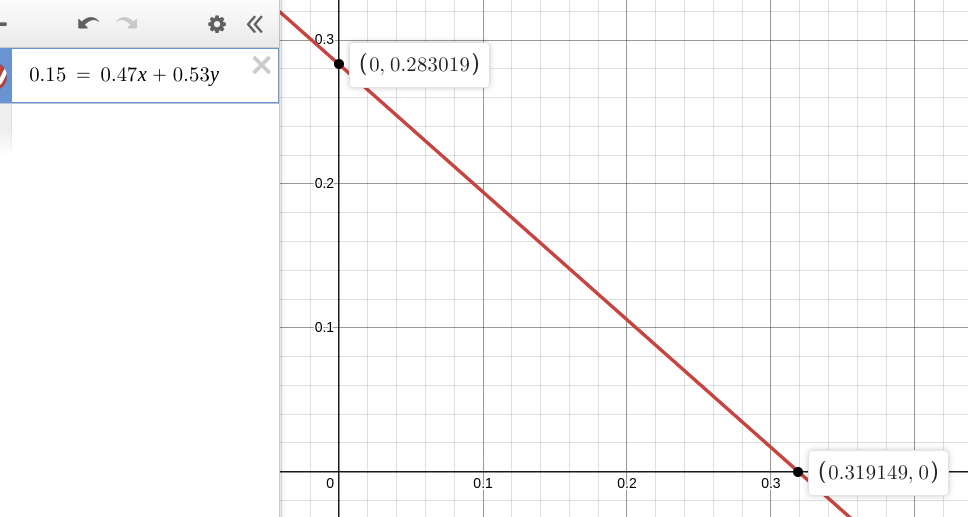
Plugging this in to our first equation above, this means that P(YES) must be at least
P(YES) ≥ 68% × 47% + 0% × 53% ≈ 32%
This is assuming that P(Elon in jail | Trump wins) = 32% and P(Elon in jail | Trump loses) = 0%. If we plug in some more reasonable numbers, say P(Elon in jail | Trump wins) = 10% and P(Elon in jail | Trump loses) = 19%, we get a higher result:
P(YES) = 90% × 47% + 19% × 53% ≈ 52%
Conversely, we can calculate the highest P(YES) can be as
P(YES) ≤ 100% × 47% + 28% × 53% ≈ 62%
Hopefully this can help others make their bets.
@bence That would not be a "correction".
This will resolve according to the logical result of the double implication, aka "iff". There's a truth table, and it's equivalent to XNOR, or with the negation of one question (as in this case) XOR of the underlyings. That is, this resolves Yes if the two underlying questions resolve differently.
There's a truth table here if that would help:
https://en.wikipedia.org/wiki/If_and_only_if#Definition
@bence And, in the common usage on this site, an "if" question would be one that resolves N/A if the precondition is false. It's a little weird to have that be different than the logical implication, IMO, but that's the common usage here. So "if", "iff", and "implies" have three different meanings. I've used "implies" where I intend that reading, rather than if, to minimize confusion.
@EvanDaniel I see, my apologies for being confused and not reading the description more carefully! I also wrote a more inquisitive comment originally acknowledging I might be wrong but was rushed and rewrote it quickly in a much worse tone.
@bence No worries, I'm happy to answer questions about my markets!
In general, I haven't found a way to write logical derivatives that are actually easy to understand when only reading the title, and wording suggestions are welcome. And sometimes the logical derivative I want isn't as simple as "and" or "or" or "resolves N/A unless the precondition happens" which are the only easy ones to title AFAICT.
@EvanDaniel Maybe you could write "Exactly one of these is true: a) Elon will spend night in jail by EOY 2026; b) Trump will win". I think this is unambiguous, but not very intuitive or catchy.
@EvanDaniel for starters, you should write "if and only if", not the niche jargon abbreviation "iff" (which most people will assume is a typo or just not notice the second F at all)